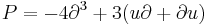Lax pair
In mathematics, in the theory of integrable systems, a Lax pair is a pair of time-dependent matrices or operators that describe the corresponding differential equations. They were introduced by Peter Lax to discuss solitons in continuous media. The inverse scattering transform makes use of the Lax equations to solve such systems.
Contents |
Definition
A Lax pair is a pair of matrices or operators 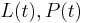 dependent on time and acting on a fixed Hilbert space, and satisfying Lax's equation:
dependent on time and acting on a fixed Hilbert space, and satisfying Lax's equation:
where ![[P,L]=PL-LP](/2012-wikipedia_en_all_nopic_01_2012/I/a9c012fcaf6078b1740a1ba30fee2eb3.png) is the commutator. Often, as in the example below,
is the commutator. Often, as in the example below,  depends on
depends on  in a prescribed way, so this is a nonlinear equation for
in a prescribed way, so this is a nonlinear equation for  as a function of
as a function of  .
.
Isospectral property
It can then be shown that the eigenvalues and more generally the spectrum of L are independent of t. The matrices/operators L are said to be isospectral as  varies.
varies.
The core observation is that the matrices 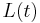 are all similar by virtue of
are all similar by virtue of
where 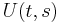 is the solution of the Cauchy problem
is the solution of the Cauchy problem
where I denotes the identity matrix. Note that if L(t) is self-adjoint and P(t) is skew-adjoint, then U(t,s) will be unitary.
In other words, to solve the eigenvalue problem Lψ = λψ at time t, it is possible to solve the same problem at time 0 where L is generally known better, and to propagate the solution with the following formulas:
 (no change in spectrum)
(no change in spectrum)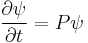
Link with the inverse scattering method
The above property is the basis for the inverse scattering method. In this method, L and P act on a functional space (thus ψ = ψ(t,x)), and depend on an unknown function u(t,x) which is to be determined. It is generally assumed that u(0,x) is known, and that P does not depend on u in the scattering region where 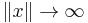 . The method then takes the following form:
. The method then takes the following form:
- Compute the spectrum of
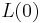 , giving
, giving  and
and 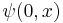 ,
, - In the scattering region where
 is known, propagate
is known, propagate  by using
by using 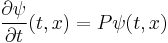 with initial condition
with initial condition 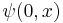 ,
, - Knowing
 in the scattering region, compute
in the scattering region, compute 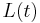 and/or
and/or 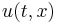 .
.
Example
The Korteweg–de Vries equation is
It can be reformulated as the Lax equation
with
where all derivatives act on all objects to the right. This accounts for the infinite number of first integrals of the KdV equation.
Equations with a Lax pair
Further examples of systems of equations that can be formulated as a Lax pair include:
- Benjamin–Ono equation
- One dimensional cubic non-linear Schrödinger equation
- Davey-Stewartson system
- Kadomtsev–Petviashvili equation
- Korteweg–de Vries equation
- KdV hierarchy
- Modified Korteweg-de Vries equation
- Sine-Gordon equation
- Toda lattice
References
- Lax, P. (1968), "Integrals of nonlinear equations of evolution and solitary waves", Comm. Pure Applied Math. 21 (5): 467–490, doi:10.1002/cpa.3160210503
- P. Lax and R.S. Phillips, Scattering Theory for Automorphic Functions, (1976) Princeton University Press.
![\frac{dL}{dt}=[P,L]](/2012-wikipedia_en_all_nopic_01_2012/I/12b14bcb8af781360a692f40874d4da7.png)
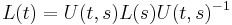
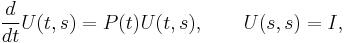
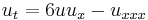
![L_t=[P,L]\,](/2012-wikipedia_en_all_nopic_01_2012/I/6230867382ccb2b1cea102c55ec95078.png)
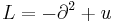 (a
(a